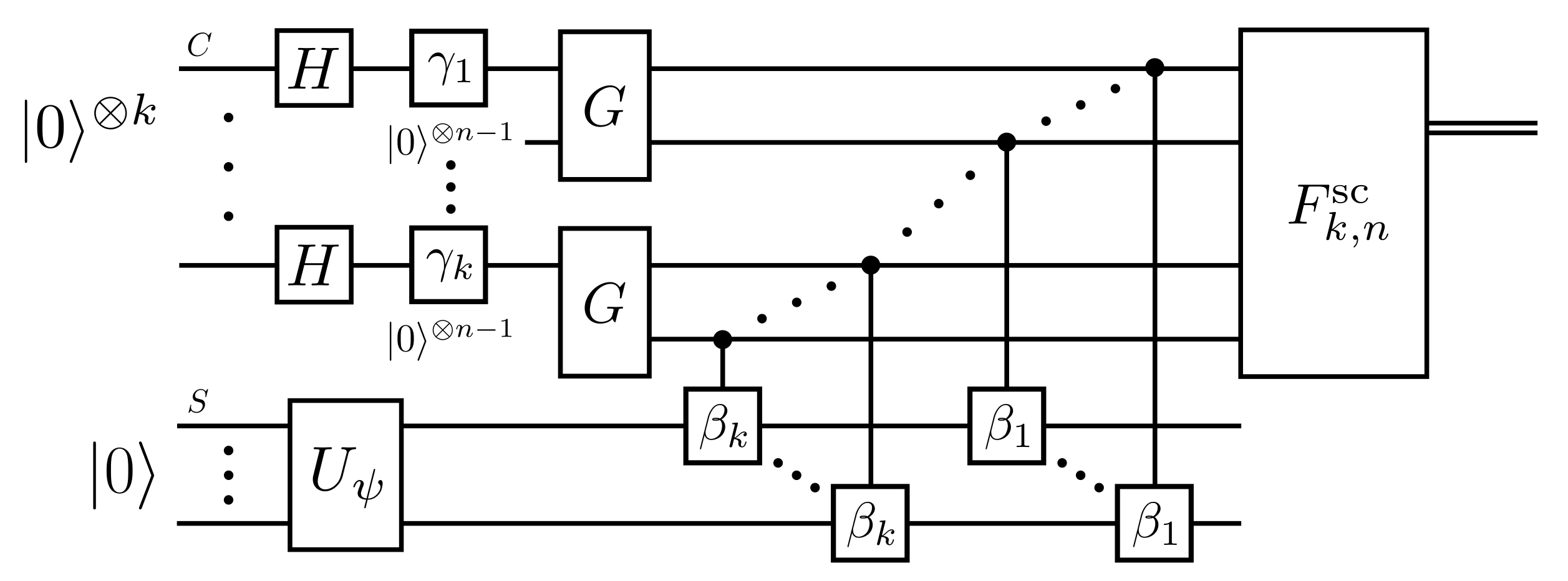
A pure state of fixed Hamming weight is a superposition of computational basis states such that each bitstring in the superposition has the same number of ones. Given a Hilbert space of the form \( \mathcal{H} = (\mathbb{C}_2)^{\otimes n}\), or an \(n\)-qubit system, the identity operator can be decomposed as a sum of projectors onto subspaces of fixed Hamming weight. In this work, we propose several quantum algorithms that realize a coherent Hamming weight projective measurement on an input pure state, meaning that the post-measurement state of the algorithm is the projection of the input state onto the corresponding subspace of fixed Hamming weight. We analyze a depth-width trade-off for the corresponding quantum circuits, allowing for a depth reduction of the circuits at the cost of more control qubits. For an \(n\)-qubit input, the depth-optimal algorithm uses \(\mathcal{O}(n)\) control qubits and the corresponding circuit has depth \( \mathcal{O}(\operatorname{log}(n)) \), assuming that we have the ability to perform qubit resets. Furthermore, the proposed algorithm construction uses only one- and two-qubit gates.